Setup

In order to calculate neighbouring polygons, we need to form a network of nodes for the data. This is done using the igraph (file. 2020) spdep (Bivand 2020) and spatialreg (Bivand and Piras 2019) packages. We also use the raster (Hijmans 2020) package to download some example data, and ggplot2 (Wickham et al. 2020) for the final visualisation.

# Loading example data
library(raster) # loads shapefile

# Data Analysis
library(igraph) # build network
library(spdep) # builds network
library(spatialreg)

# Visualisation
library(RColorBrewer)  # for plot colour palette
library(ggplot2) # plots results
library(tmap)

First downloading the data as follows. The input data is shown in Figure 1. You could easily provide your own shapefile here instead or run the code for a different country by changing the three-digit code. For my example, I have selected Hungary:

# Load Data
boundaries <- raster::getData(name = "GADM", country = "HUN", level = 2)

# Show data
tm_shape(boundaries) +
  tm_polygons()

Figure 1: Loaded data for the raster package

Extracting neigbours

Firstly the poly2nb function is used to calculate neighbouring regions, based on contiguous boundaries, that is sharing one or more boundary point. The resulting mesh and coordinates is shown in Figure 2

# Find neighbouring areas
nb_q <- poly2nb(boundaries)

# Plot original results
coords <- coordinates(boundaries)

# Show the results
plot(boundaries)
plot(nb_q, coords, col="grey", add = TRUE)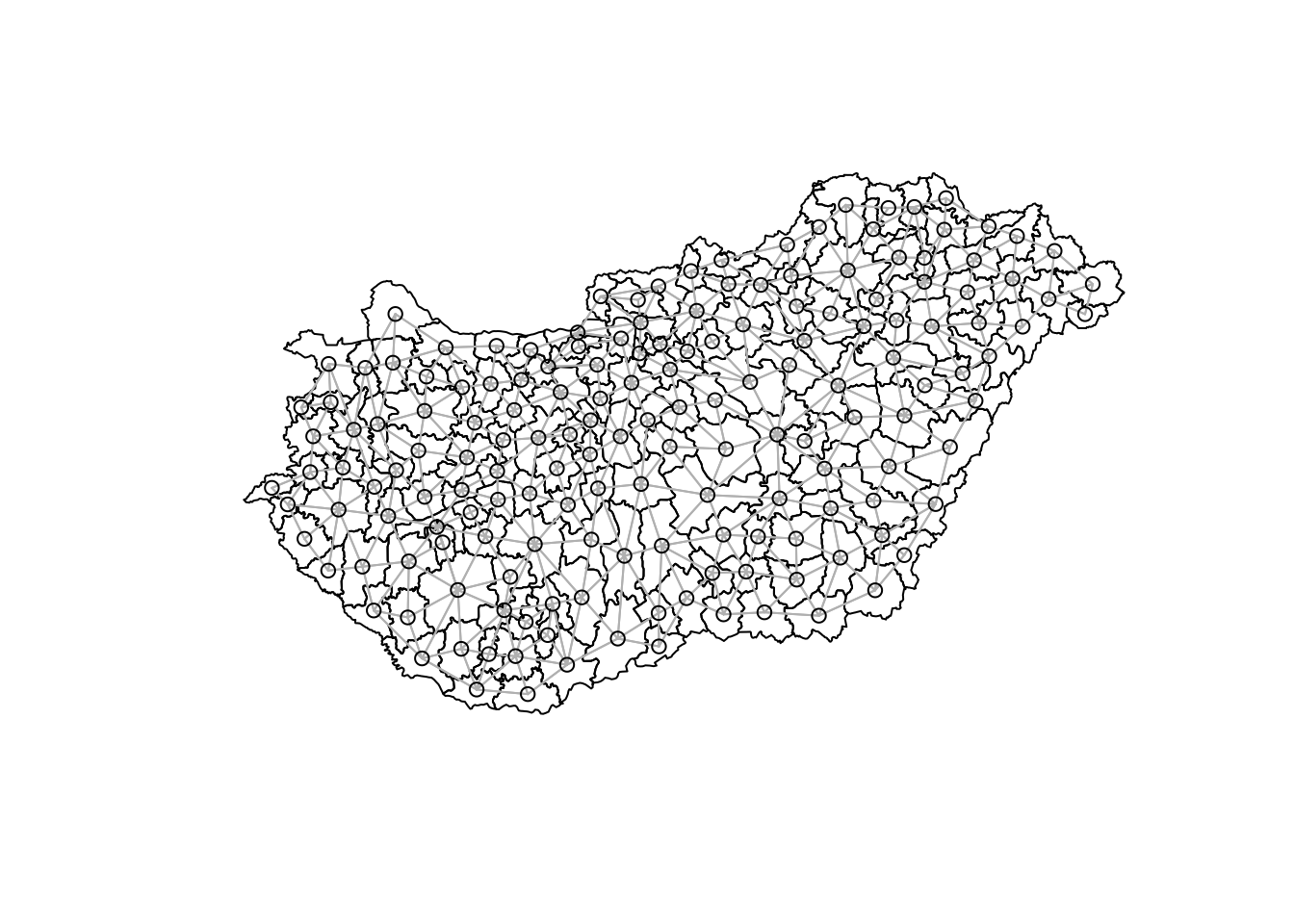

Figure 2: Mesh outputs from poly2nb

With this mesh, we can then calculate the shortest path between two locations. The follow function returns a list for each and every pair of polygons.

# Sparse matrix
nb_B <- nb2listw(nb_q, style="B", zero.policy=TRUE)
B <- as(nb_B, "symmetricMatrix")
    
# Calculate shortest distance
g1 <- graph.adjacency(B, mode="undirected")
sp_mat <- shortest.paths(g1)

Having made the calculations, the data can now be formatted to get into plotting format, so the shortest path matrix is merged with the spatial dataframe.

# Name used to identify data
referenceCol <- boundaries$GID_2
  
# Rename spatial matrix
sp_mat2 <- as.data.frame(sp_mat)
sp_mat2$id <- rownames(boundaries@data)
names(sp_mat2) <- paste0(referenceCol)
          
# Add distance to shapefile data
boundaries@data <- cbind(boundaries@data, sp_mat2)
boundaries@data$id <- rownames(boundaries@data)

The data is now in a suitable format to display. Using the basic function spplot we can get a graph quite quickly:

tm_shape(boundaries) +
  tm_polygons("HUN.15.5_1", n = 15)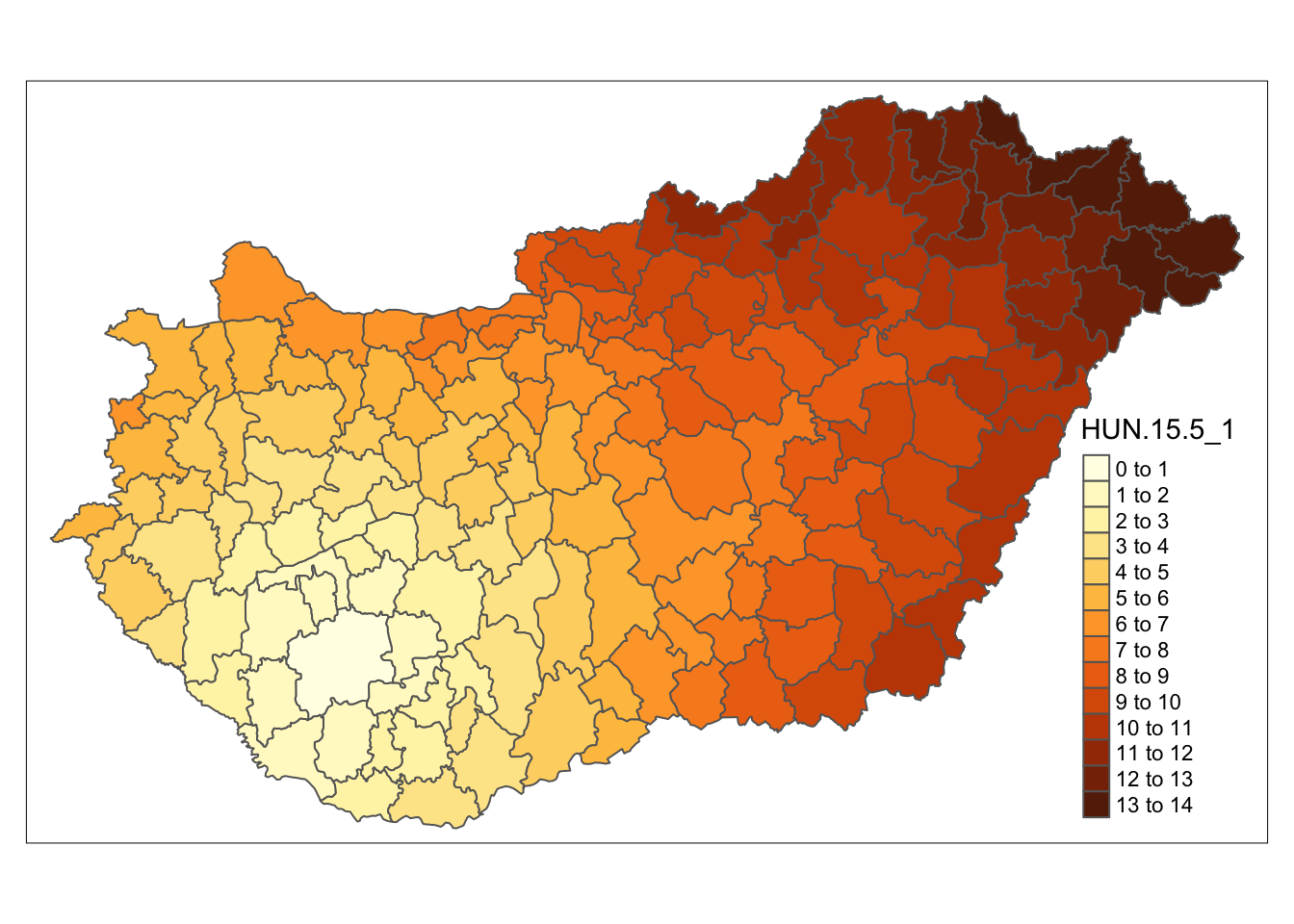 

Plotting in ggplot2

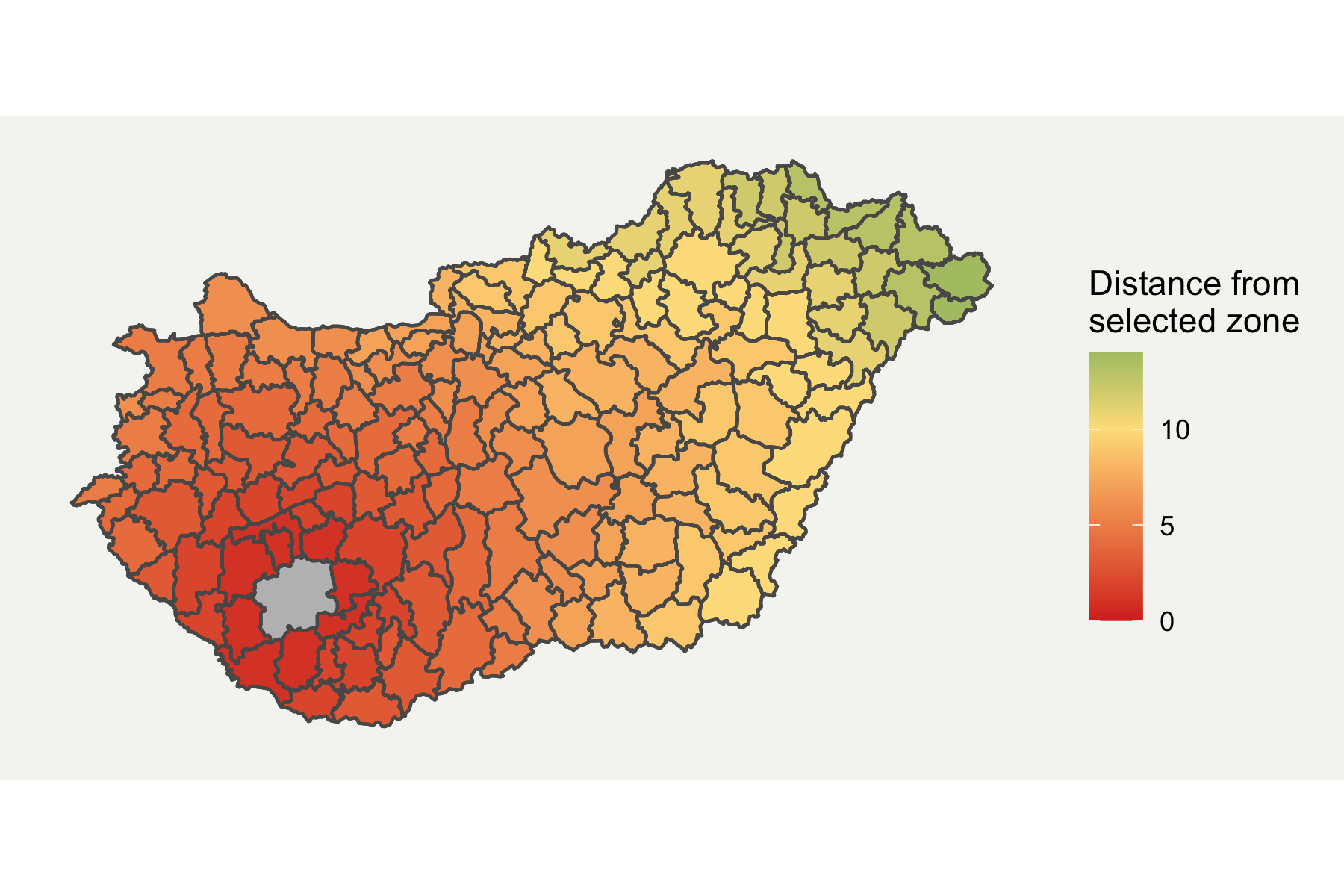
I prefer ggplot for plotting more complex graphs as you can control the styling easier. Fortunately, ggplot2 now directly supports spatial data through geom_sf format. I have customised it a bit by removing elements which aren’t required and added a background. The final map is shown below in Figure 3.

# Convert data to sf format
boundaries_sf <- sf::st_as_sf(boundaries)

ggplot(boundaries_sf) +
  geom_sf(aes(fill = HUN.15.5_1)) +
  geom_sf(fill = "grey", alpha = ifelse(boundaries_sf$GID_2 == "HUN.15.5_1", 1, 0)) +
  scale_fill_gradient2(low = "#d73027", mid = "#fee08b", high = "#1a9850", midpoint = 10) +
  labs(fill = "Distance from \nselected zone") +
  theme(
    axis.line = element_blank(),
    axis.text.x = element_blank(),
    axis.text.y = element_blank(),
    axis.ticks = element_blank(),
    axis.title.x = element_blank(),
    axis.title.y = element_blank(),
    panel.grid.minor = element_blank(),
    panel.grid.major = element_blank(),
    plot.background = element_rect(fill = "#f5f5f2", color = NA), 
    panel.background = element_rect(fill = "#f5f5f2", color = NA), 
    legend.background = element_rect(fill = "#f5f5f2", color = NA),
    panel.border = element_blank())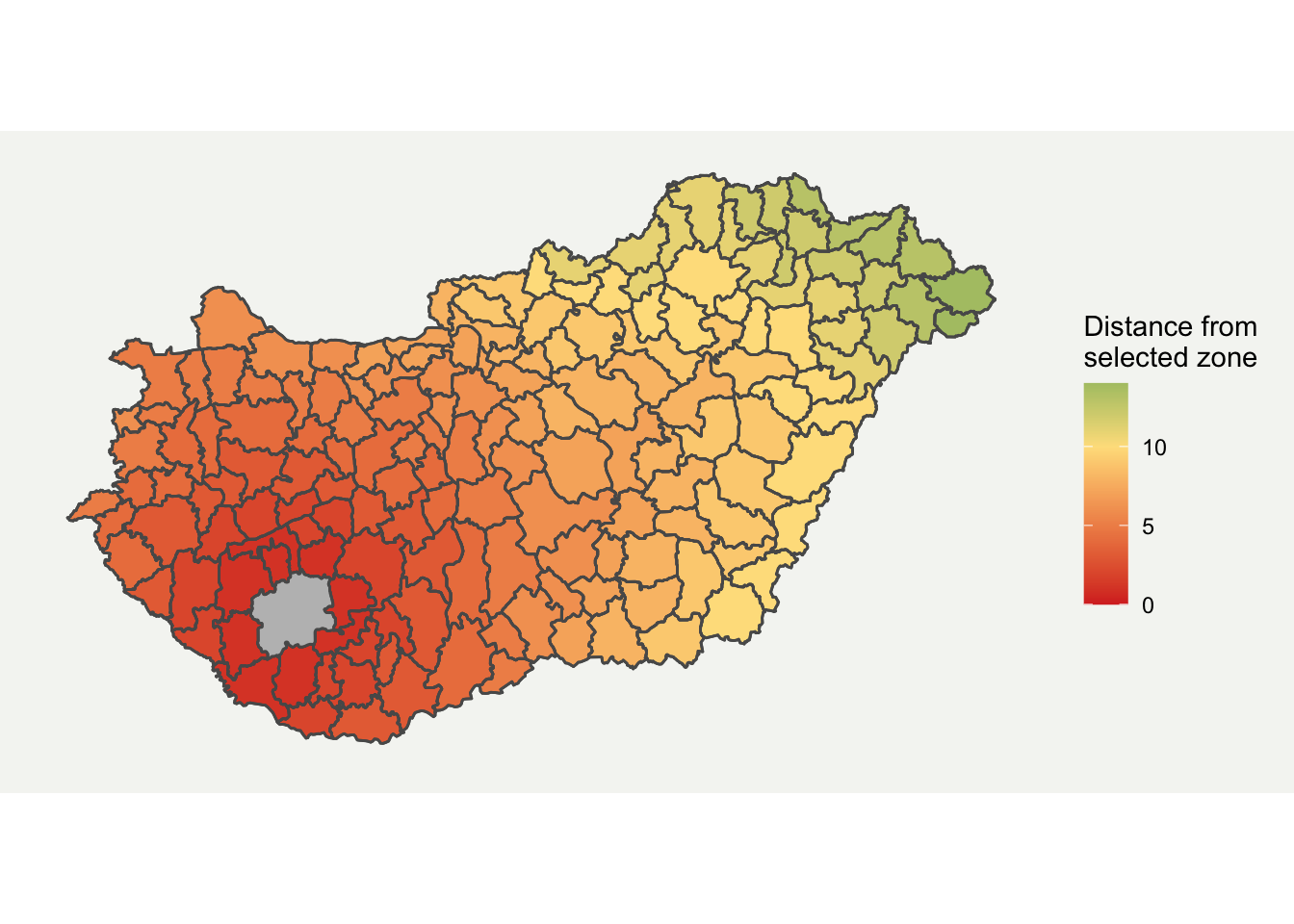

Figure 3: Final Neighbouring Region Map